백준 정렬문제를 쭈욱 풀면서 10989 번 문제를 풀게 되었는데, 이전의 풀이 식으로 문제를 풀이하니 전혀 메모리초과.. 와 같은 문제가 발생했다 ㅜ.ㅜ
나와 같은 문제를 겪는 사람들이 있을까 하여 질문글들을 찾아보니, 이런 문제의 경우에는 카운팅정렬을 사용할 것을 추천하는걸 보고 '카운팅정렬' 알고리즘을 공부 !_!
'빠른 속도'를 자랑하는 정렬 알고리즘으로는 시간복잡도가 O(N*logN)의 속도를 가지는 퀵정렬, 병합정렬, 힙 정렬 등이 있다.
하지만, 이보다 더 빠른속도의 정렬 알고리즘이 필요하다면? 특정한 조건을 만족하는 상황에서 시간복잡도가 무려 O(n)인 빠른 정렬 알고리즘인 '카운팅정렬(Counting Sort)'를 정리하고자 한다.
1. 카운팅 정렬
정렬하고자하는 모든 데이터가 특정 범위조건 안에 있는 경우, 각 데이터 값마다 등장하는 횟수를 세는것으로 정렬하는 알고리즘이다. 다른 정렬 알고리즘은 데이터들끼리 크기를 비교하여 자리를 옮기는 방식으로 정렬을 하였지만, 카운팅정렬은 자리를 바꿔줄 필요도 없고 각 데이터에 한번씩 접근하여 등장횟수만을 Counting 하면 되기 때문에 훨씬 빠르고 효율적이다!
이렇게 말하면 한번에 와닿기 어려울 수 있기에 예시와 함께 설명하겠다!
▶ 5, 2, 3, 1, 4, 2, 3, 5, 1, 7 , 2, 4, 6, 8, 1, 9, 4, 2, 7, 5 를 오름차순으로 정렬하시오
위의 자연수들은 모두 1부터 9사이의 범위 안에 있다는 공통점이 있다. 따라서, 데이터들의 등장횟수를 저장할 '크기가 9인 배열 count'를 선언하여 저장해주고자 한다. count[]의 각 원소의 값에는 대응되는 데이터값의 등장 횟수를 저장한다.
데이터 배열의 맨 앞부터 순서대로 접근한다.
(0) 초기상태
배열 count의 값들이 모두 0으로 초기화 되어있는 상태이다.
5, 2, 3, 1, 4, 2, 3, 5, 1, 7 , 2, 4, 6, 8, 1, 9, 4, 2, 7, 5
| count[1] | count[2] | count[3] | count[4] | count[5] | count[6] | count[7] | count[8] | count[9] |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
(1)-1번째 접근
1번째 데이터는 5이므로, count[5]에 값을 1 증가시켜준다.
5, 2, 3, 1, 4, 2, 3, 5, 1, 7 , 2, 4, 6, 8, 1, 9, 4, 2, 7, 5
| count[1] | count[2] | count[3] | count[4] | count[5] | count[6] | count[7] | count[8] | count[9] |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
(1)-2번째 접근
2번째 데이터는 2이므로, count[2]에 값을 1 증가시켜준다.
5, 2, 3, 1, 4, 2, 3, 5, 1, 7 , 2, 4, 6, 8, 1, 9, 4, 2, 7, 5
| count[1] | count[2] | count[3] | count[4] | count[5] | count[6] | count[7] | count[8] | count[9] |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
(1)-3번째 접근
3번째 데이터는 3이므로, count[3]에 값을 1 증가시켜준다.
5, 2, 3, 1, 4, 2, 3, 5, 1, 7 , 2, 4, 6, 8, 1, 9, 4, 2, 7, 5
| count[1] | count[2] | count[3] | count[4] | count[5] | count[6] | count[7] | count[8] | count[9] |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
(2)결과
이쯤되면 마지막 데이터에 접근했을때의 count 배열의 결과가 보일 것이다!
| count[1] | count[2] | count[3] | count[4] | count[5] | count[6] | count[7] | count[8] | count[9] |
| 3 | 4 | 2 | 3 | 3 | 1 | 2 | 1 | 1 |
따라서, count배열에는 각 원소의 개수가 저장되어 있으므로, 원소 i를 count[i]만큼 반복하여 출력하면 아래와 같이 카운팅 정렬이 완성된다!
▶1 1 1 2 2 2 2 3 3 4 4 4 5 5 5 6 7 7 8 9
카운팅 정렬이 무엇인지 알아보았으니, 카운팅 정렬 알고리즘을 이용하는 문제인 백준 10989번을 풀어볼 차례이다.
2. 백준 10989번
https://www.acmicpc.net/problem/10989
10989번: 수 정렬하기 3
첫째 줄에 수의 개수 N(1 ≤ N ≤ 10,000,000)이 주어진다. 둘째 줄부터 N개의 줄에는 수가 주어진다. 이 수는 10,000보다 작거나 같은 자연수이다.
www.acmicpc.net
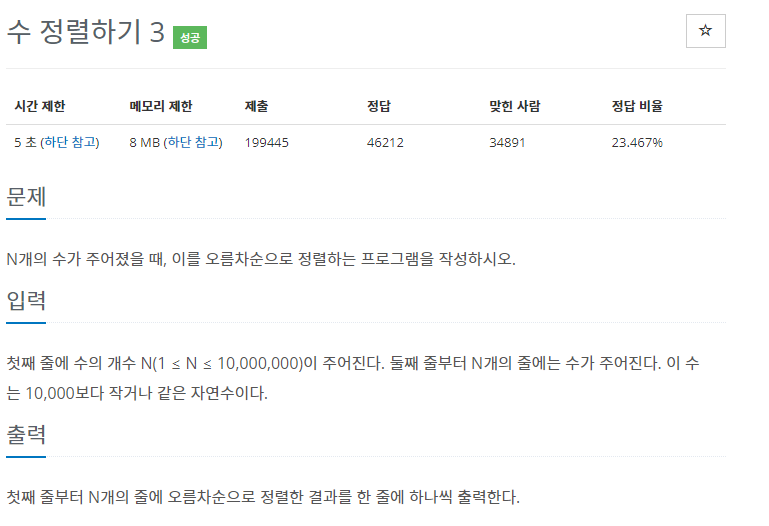
입력조건을 살펴보면, 입력되는 수들은 '10,000보다 작거나 같은 자연수'라는 범위 조건을 갖고있다.
아하! 크기가 10001인 count배열을 만들어 입력되는 데이터들의 등장횟수를 저장하면 되겠다.
시간제한이 5초인 만큼, 이 문제를 풀면서 시간초과로 문제를 틀리고 알게된 방법
입출력의 수가 많을 때는 (시간복잡도와 별개로 입출력이 실행 속도에서 차지하는 비중이 꽤 크다고 한다.)
메인함수 최상단에 아래와 같은 문구를 추가하여 빠른 입출력을 유도해주는 것이 좋다
ios_base::sync_with_stdio(false);
cin.tie(NULL); count.tie(NULL);
위 문구를 추가한다는 것은, c언어 표준 스트림버퍼와의 동기화를 끊는다는 것을 의미한다. 이에따라 c++만의 독립적인 버퍼를 갖게되며 C의 입출력 방식은 사용할 수 없게 된다.(scanf(), printf(), fgets(), getchar() 등등) 또한 cin은 기본적으로 cout에 종속되어 있는데, 이 또한 위 문구를 추가해 줌으로써 각각을 분리해주게 된다.
(위 문구를 추가한 c++17은 거의 모든 언어 입출력 속도 순위에서 최상위권에 위치한다.)
출처: https://www.acmicpc.net/board/view/96901
<백준 10989번 소스코드>
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
#include <iostream>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
int N, input;
int count[10001] = { 0, };
cin >> N;
for (int i = 1; i <= N; i++) {
input = 0;
cin >> input;
count[input]++;
}
for (int i = 1; i <= 10000; i++) {
if (count[i] != 0) {
for (int k = 0; k < count[i]; k++) {
cout << i << "\n";
}
}
}
return 0;
}
|
cs |
'알고리즘' 카테고리의 다른 글
| [백준 10799] 쇠막대기 (stack 활용) (3) | 2022.11.29 |
|---|---|
| [백준 9012] 괄호 (stack활용) (0) | 2022.11.28 |
| [백준 11052] 카드 구매하기 (DP, 점화식) (4) | 2022.10.29 |
| [백준 1912] 연속 합 (DP, 점화식) (0) | 2022.10.24 |
| [백준 2579] 계단 오르기 (DP, 점화식) (2) | 2022.10.18 |