오랜만에 블로그 들어왔는데 스킨이 초기화 되어있어서 깜짝놀랐,,,
카카오 오류 때문에 아직 스킨은 복구중이라는데 어후 내거만 이상해진줄 알고 놀랐네 휴
티스토리 일ㅇ하자...
https://www.acmicpc.net/problem/2579
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
문제
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.

예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.
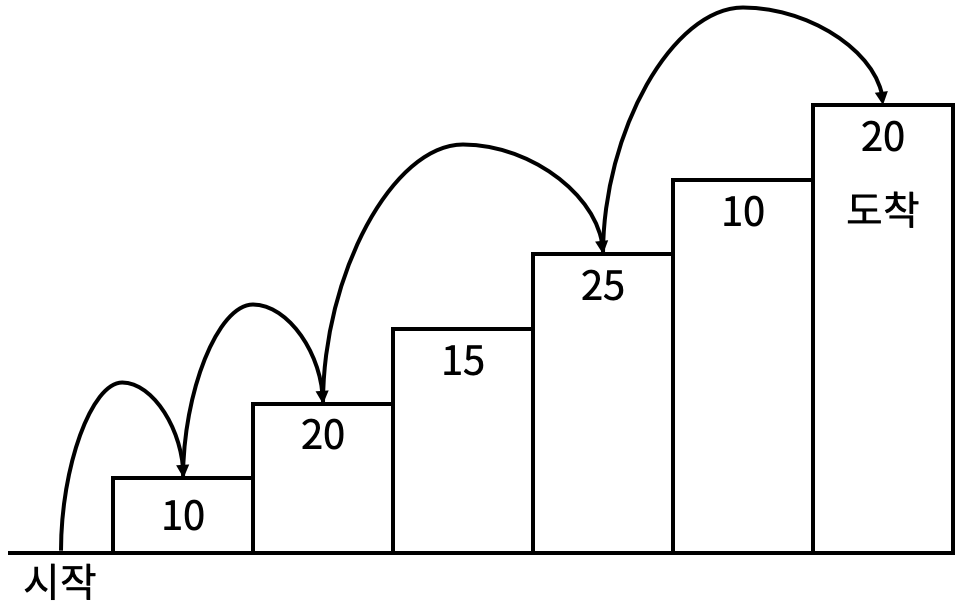
계단 오르는 데는 다음과 같은 규칙이 있다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
예제 입력
6
10
20
15
25
10
20
예제 출력
75
1번째 계단부터 N번째 계단까지 각 계단의 점수를 배열 arr[i]에 저장하고, i번째 계단일때의 최대점수를 배열 dp[i]에 각각 저장한다고 하자.
n=1일때부터 살펴보면
n=1일때, dp[1] = arr[1]
n=2일때, dp[2] = arr[1] + arr[2] (* arr[1]보다 arr[1] + arr[2]가 무조건 더 큰 값이므로)
n=3일때, dp[3] = max(arr[1] + arr[3], arr[2] + arr[3])
n=4일때, dp[4]는 (1)-(2)-(4) OR (2)-(4) OR (1)-(3)-(4) 세 가지 경우의 수가 있다.
이때 (1)-(2)-(4)는 (2)-(4)의 경우에 포함된다. 즉, 두번째 계단 앞에 어떤 점수가 왔었든 상관없이, 두번째 계단까지 오는 최고점수에 (4)번 계단의 값을 더한 것과 같다.
따라서 dp[4]는 (2까지오는 최고점수)-(4) OR (1)-(3)-(4) 두가지 경우 중 큰 값을 갖는다.
dp[4]일때의 식은 잠시 뒤에서 살펴보자.
n=5일때, dp[5]는 (1)-(3)-(5) OR (2)-(3)-(5) OR (1)-(2)-(4)-(5) OR (2)-(4)-(5) 네 가지 경우의 수가 있다.
가능한 경우의 수가 많아 보이지만, 앞의 두개 경우와 뒤에 두개 경우가 각각 겹치는 부분이 존재한다는 것을 알 수 있다.
즉, (3까지오는 최고점수)-(5) OR (2까지오는 최고점수)-(4)-(5) 총 두가지 경우만이 존재하며
식으로 나타내면 dp[5] = max(dp[3] + arr[5], dp[2] + arr[4] + arr[5]) 과 같다.
마찬가지로 dp[4]도 dp[4] = max(dp[4] + arr[6], dp[3] + arr[5] + arr[6]) 로 식을 쓸 수 있다.
마지막 계단은 무조건 밟아야 한다.
n=6일때 dp[6]은 ---(4)-(6)과 ---(3)-(5)-(6) 두가지 경우가 있다. (*(3)-(4)-(6)의 경우는 (4)-(6)에 포함되므로 따로 카운트 하지 않는다.)
이를 통해 i번째 계단으로 향하는 경우의 수들은 모두 두 가지 경우로 분류할 수 있다는 것을 알 수 있다.
따라서 두가지 경우의 점수를 비교하여 둘중 더 큰 값이 최대 점수가 된다.
점화식으로 나타내면, 아래와 같이 나타낼 수 있다.
dp[i] = max(dp[i-2] + arr[i], dp[i-3] + dp[i-1] +dp[i])

백준 2579번 소스코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int max(int n1, int n2) {
return n1 > n2 ? n1 : n2;
}
int main(void)
{
int n; //300보다 작다
//계단의 개수는 300이하, 계단에 쓰여있는 점수는 10000점 이하
int arr[301] = { 0, };
int dp[300] = { 0, };
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", &arr[i]);
}
dp[1] = arr[1];
dp[2] = max(arr[1], arr[1] + arr[2]);
dp[3] = max(arr[1] + arr[3], arr[2] + arr[3]);
for (int i = 4; i <= n; i++) {
dp[i] = max(dp[i-2] + arr[i], dp[i-3] + arr[i-1] + arr[i]);
}
printf("%d", dp[n]);
return 0;
}
|
cs |
'알고리즘' 카테고리의 다른 글
| [백준 11052] 카드 구매하기 (DP, 점화식) (4) | 2022.10.29 |
|---|---|
| [백준 1912] 연속 합 (DP, 점화식) (0) | 2022.10.24 |
| [백준 10844, 11057] 쉬운 계단 수, 오르막 수 (DP, 점화식) (2) | 2022.10.12 |
| [백준 11726, 11727] 2XN 타일링 (DP, 점화식) (3) | 2022.10.11 |
| [백준 1463] 1로 만들기 (DP, 점화식) (0) | 2022.10.10 |